
Strategize – Optimize – Profitize
Website not in your language ? Right-click anywhere on the page and select ‚Translate‘ from your browser’s menu.
Businesses optimize results
Business management and strategy ever since focus on the optimization of results :
- minimization of efforts & cost and
- maximization of sales & profit
are two sides of the same medal.
Nevertheless traditional and contemporary methods are limited w.r.t. their effectiveness – real optimization mostly happens in Supply Chain Management and Operations (JIT etc.), especially in recurring business. Strategic and operative marketing und sales management today still contain huge potentials regarding results optimization.
Today’s digitalization and Industry 4.0 provide the means for any business to scale the effectiveness of their management methods and to achieve significant better results.
Optimization – the targets
Optimization adresses measures for the improvement of an actual state towards the best possible state – the optimum. It can be either a minimum or a maximum.
In economics and in management typical (simple … ) optimization targets may be :
- Minimization of inputs
e.g. minimization of efforts, stocks, times, ressources, risiks or the like - Maximization of outputs
e.g. maximization of sales, results, profits etc.
In ‚real-world‘ management things are not so simple : optimization targets not always are obvious and unique; one may have to deal with :
- Multiple objectives
exist almost always; in this case multi-objective optimization techniques must be applied - Conflicting targets
may pose contradicitng requirements to an optimization solution - Causality
objectives should be subject of reasonable cause-and-effect relations - Hierarchy
Targets should have a hierarcical-causal realtions to each other (as in cascaded metrics systems, e.g. DuPont or TEEP/OEE) - Constraints
of all kinds may exist (w.r.t. time, procedural, resources etc.) - Complexity
the target system’s complexity may be high - Dynamics
targets may vary with time; dynamic optimization techniques may be required instead of static approaches - Observeability and Steerability
the objectives should be observable (visible) and steerable (influenceable)
As early as in the pre-optimization phase, setting up a coherent system of (management-) objectives may pose a major challenge, as is known by those, who have already managed major / large scale Balanced Scorecard projects.

Optimization – Players and Methods
Two kinds of players optimize in Profitable Growth Management : men and machines.
Humans (managers) – acting as optimizers – may apply the following techniques :
- Trial and error
widespread principle, may work, may not work, resources intense, lengthy, error-prone, may not converge - Common sense
works somewhat with clear / obvious problems, especially for cases where problem and experience do match (deja vu); slow.
Often gutt feeling dominates common sense (decide on feelings and justify with facts … ) - Methods
the effectiveness of setting up and applying principles, as well as catalogues of dos and don’ts is well known … - Manual Analytics
e.g. manual calculations, works with very simple challenges; slow and error-prone
Computers as optimization engine work based on numerical optimization methods; these are fast, reproduceable und scaleable.
Modern numerical optimization methods are able to adress all strategy drivers (complexity, uncertainty ec.).
In case a target function is defined (Profitable Growth … ), the following optimization methods can be applied :
- Linear Optimization
Operations research method, which works with linear target functions, linear equations and inequalities. - Stochastic gradient descent
is an iterative optimization algorithm commonly used in machine learning to find the parameters of a model that minimize a given loss function. It works by estimating the gradient of the loss function using a small random sample of the training data, and then updating the model parameters in the direction of the negative gradient. - Non-linear Optimization
mathematical OR method working with non-linear targets functions and constraints. Applicable to differentiable non-linear target functions. Frequently used is the Marquardt-Levenberg algorithm. - Dynamic Programming
Optimization algorithm which aims at simplifying a complicated problem by breaking it down into simpler sub-problems in a recursive manner. Invented by nach Richard Bellman. - Stochastic Optimization
these are optimization methods that generate and use random variables. For stochastic problems, the random variables appear in the formulation of the optimization problem itself, which involve random objective functions or random constraints (Simulation, Monte-Carlo Methods) - Heuristics
are approaches to problem solving, learning, or discovery that employs a practical method, not guaranteed to be optimal, perfect, logical, or rational, but instead sufficient for reaching an immediate goal. Universal heuristics (meta heuristics) are e.g. ant colony algorithm, evolutionary algorithm (genetic algorithm), simulated annealing and taboo search - Genetic Algorithms
is a metaheuristic inspired by the process of natural selection that belongs to the larger class of evolutionary algorithms (EA). Genetic algorithms are commonly used to generate high-quality solutions to optimization and search problems by relying on bio-inspired operators such as mutation, crossover and selection - Particle Swarm Optimization
is a computational method that optimizes a problem by iteratively trying to improve a candidate solution with regard to a given measure of quality. It solves a problem by having a population of candidate solutions, here dubbed ‚particles‘ - Bayesian Optimization
utilizes probabilistic models to predict the performance of different solutions, focusing its search on the most promising areas of the parameter space and efficiently handling expensive-to-evaluate functions. This makes it particularly well-suited for complex tasks like hyperparameter tuning in machine learning models.
Especially powerful are the high performance methods as used in Machine Learning for Artificial Intelligence (AI) (see next page)
Example : Gradient descent
Optimimization algorithms show a wide range of performances (w.r.t. accuracy, convergence, computer time etc.); the animation (right side chart ) illustrates the convergence of some well known optimization methods by use of a simple 2-dimensional example, beginning with ‚Stochastic Gradient Descent‘ (SGD ) as the slowest method up to ‚Adaptive Subgradient Method‘ (ADAGRAD) as (one of) the fastest method(s). Already this very basic example shows performance differences varying by a factor of 100.

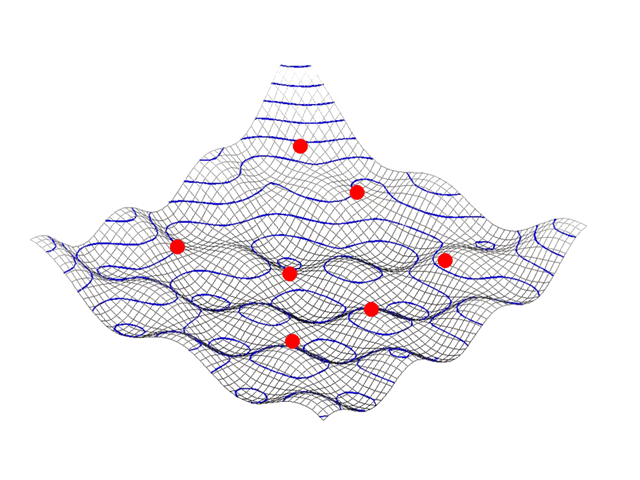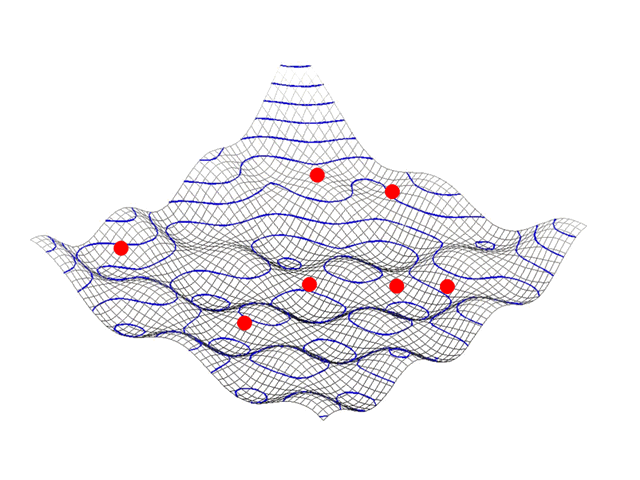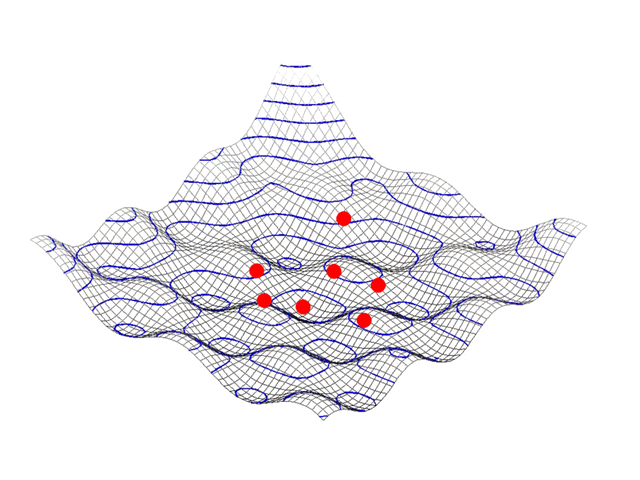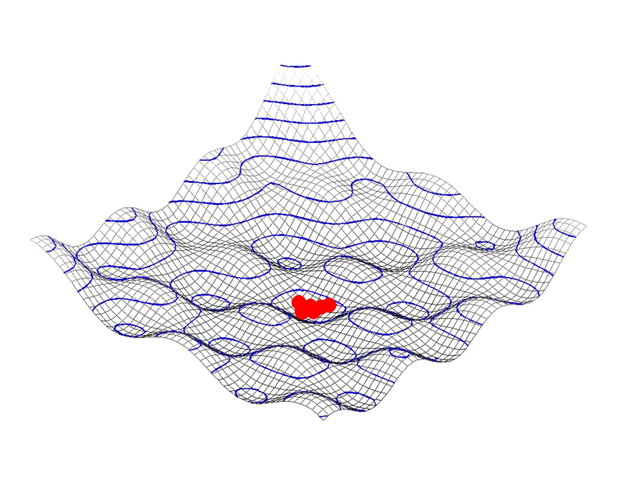
Example : Particle Swarm Optimization
The graphics at the left shows an example of Particle Swarm Optimization.
A two dimensional target function describes the depedency between e.g. profitability versus growth.
Multiple random solutions (red bullets) converge towards a local profit-growth optimum.
Example for Optimization in Management : the Traveling Sales Man Problem
A classic example for an application of OR-like optimization methods in management is the ‚Traveling Sales Man‘ problem : a sales rep faces the mission to visit a larger number of customer locations in a single trip; the travel shall start and end at it’s home location. The total distance traveled shall be minimal.
The two graphics below show an illustrative, ficticious example : the travel of a sales rep along the largest cities in the USA and Canada; the travel has to be realized at a minimum total distance traveled. The graphics on the left shows the travel route minimization by means of a genetic algorithm; the graphics on the right shows the solution : the minimum distance travel path.


(Source: https://blogs.mathworks.com/pick/2011/10/14/traveling-salesman-problem-genetic-algorithm/; Autor : Will Campbell, 2011)
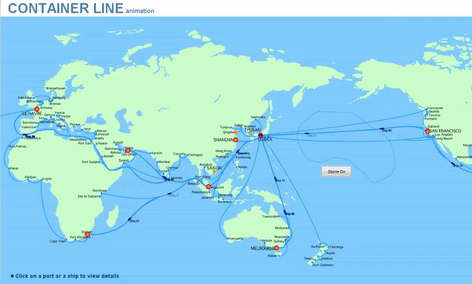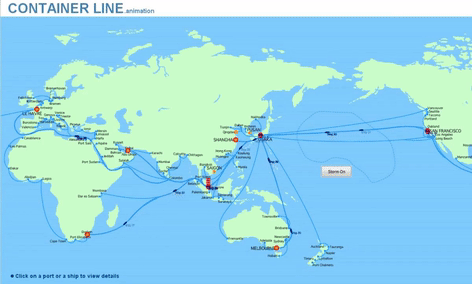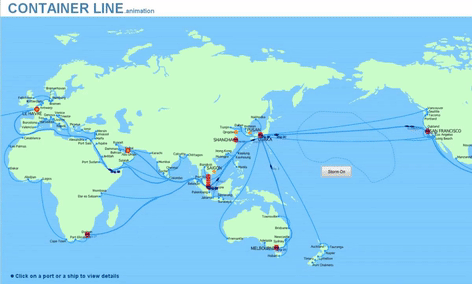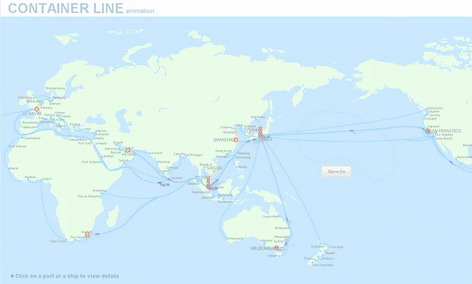
Example for Optimization in Management : Supply Chain Management
The conceptual low-scale example of the ‚traveling sales man‘ optimization can be extended to large scales when e.g. transitioning to Supply Chain Management.
The same or similar optimization methods can be applied to optimize the transport routes of containers in sea transport and land transport.
Optimization criteria may be minimum transport distances, minimum transport cost, minimum transport times or combinations of these (multi objective optimization).
…

